24-空间变换—三维

三维坐标系类型

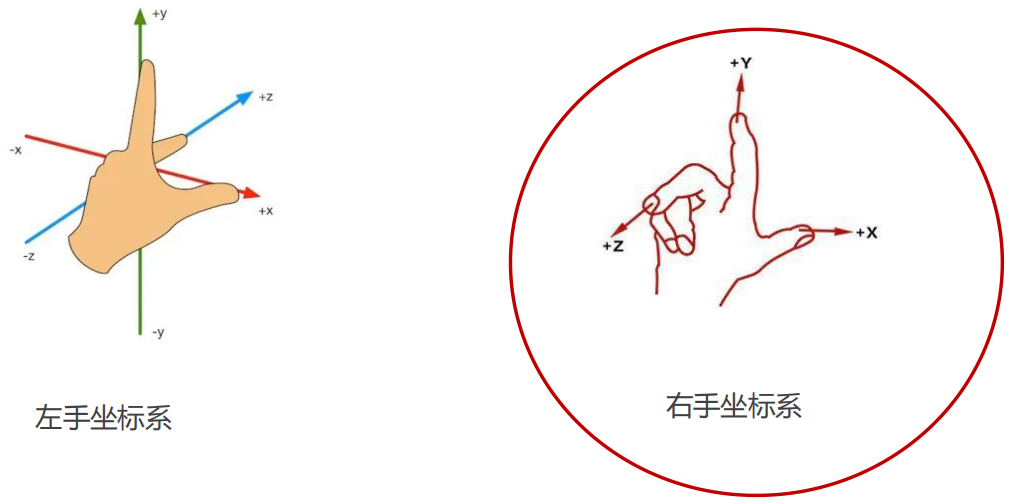
三维坐标系基向量(X/Y/Z) 根据排列不同，分为左手坐标系与右手坐标系，OPengl采用的是右手坐标系

三维变换

三维空间变换是三维向量与3*3矩阵的关系，由于存在平移变换需求，也需要增加一个维度，变为四维

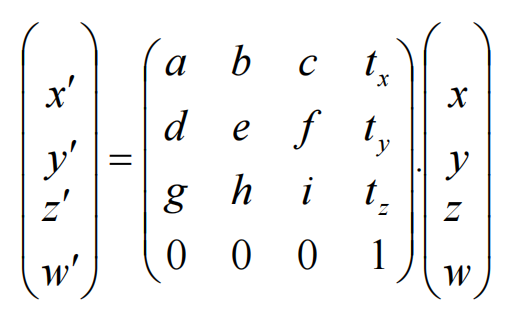
平移矩阵与缩放矩阵

平移与缩放，二维和三维差不多，只是增加了矩阵维度

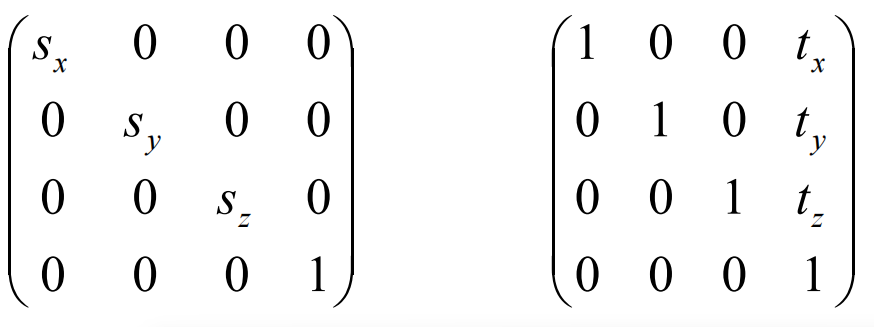
旋转矩阵

对于三维空间的旋转，并不是围绕一个点，而是围绕一个旋转中心轴，最简单的三维旋转就是分别绕三个基向量(x/y/z轴)进行旋转

旋转规则

对于绕某个轴旋转时，是指逆着当前轴看过去，让该轴正指向自己，逆时针旋转角度

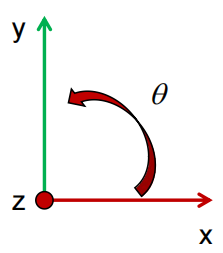
对照二维旋转

二维旋转可以理解为任意两个相互垂直的向量作为坐标轴，逆时针旋转某一角度的结果

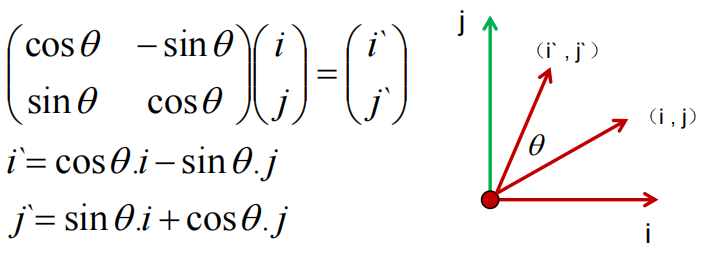
三维旋转按照X/Y/Z旋转，可以看作让某两个轴作为上面的i与j

绕Z轴旋转

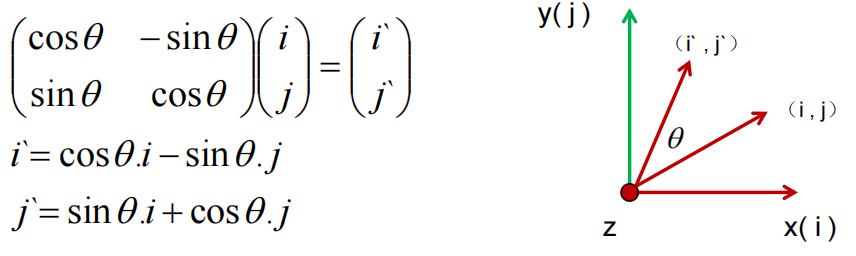
构造出如下旋转矩阵：

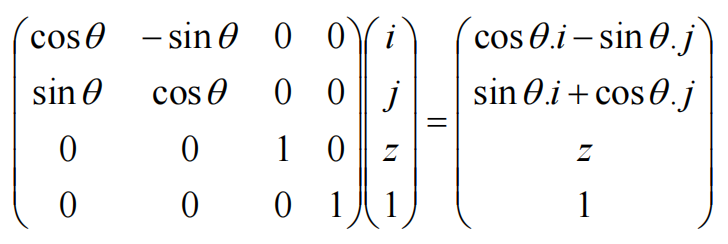
绕X轴旋转

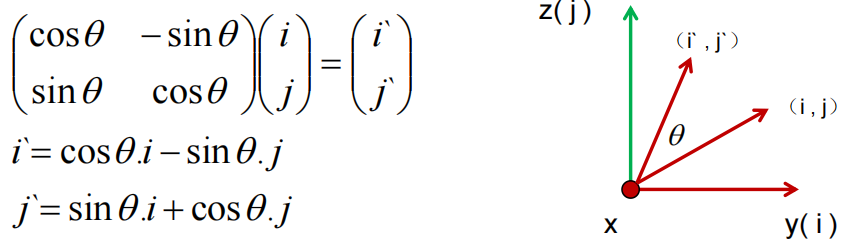
构造出如下旋转矩阵：

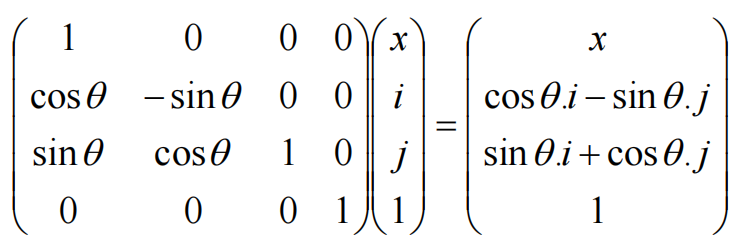
绕Y轴旋转

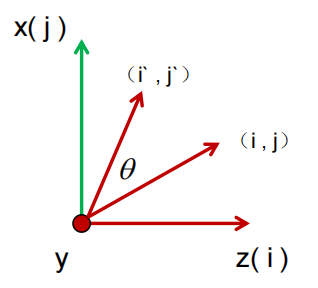
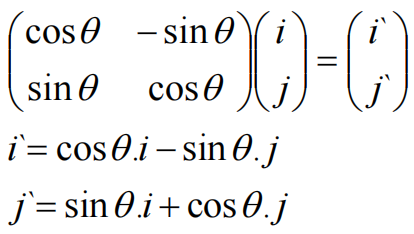
构造出如下旋转矩阵：

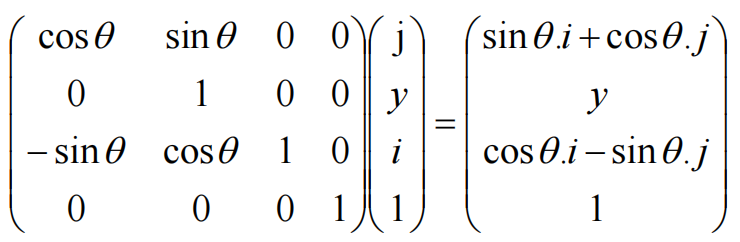
总结