目标分析

分析对于一个Mesh的一次Draw调用，其中的三角形会产生以下三种情况

图-1

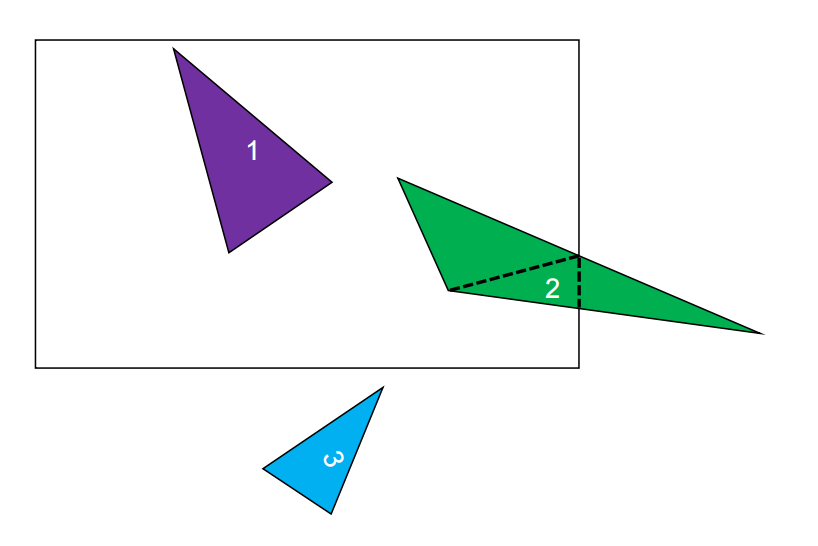
1.三角形在可视范围内，顶点都保留
2.三角形在与视范围相交，去掉外围点，产生新点
3.三角形不在可视范围内，丢弃所有顶点

Sutherland-Hodgman算法

也叫逐边剪裁法，该算法采用了分割处理、逐边剪裁的方法

算法思想（二维）
一次用窗口的一条边所在直线裁剪多边形，循环多次；
每次，构造一个空的点数组DST；原数组为SRC
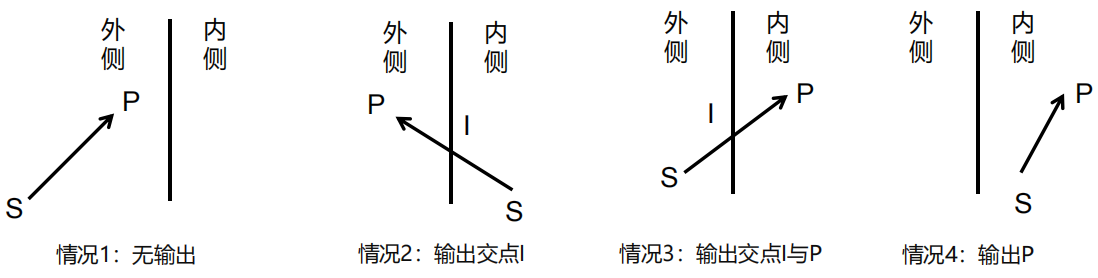
每次，所有顶点从0号开始，作为S点，S后面的点为P点，依次进行测试，结果输出点到DST，剪裁原则如下：

图-2

Sutherland-Hodgman算法举例演示（1）

输入0-1-2考察右侧边

图-3

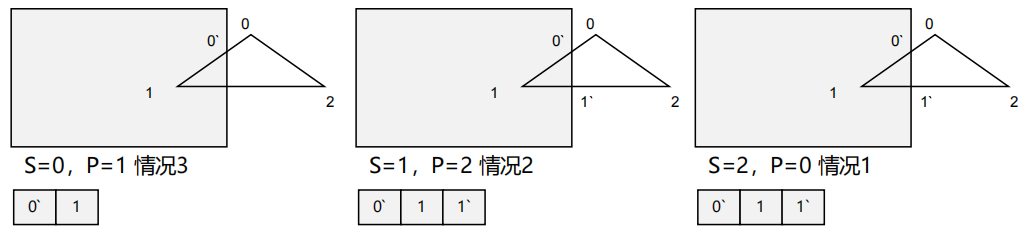
如法炮制考察剩余三边后，输出三角形0`-1-1`的点

Sutherland-Hodgman算法举例演示（2）

输入0-1-2考察上侧边

图-4

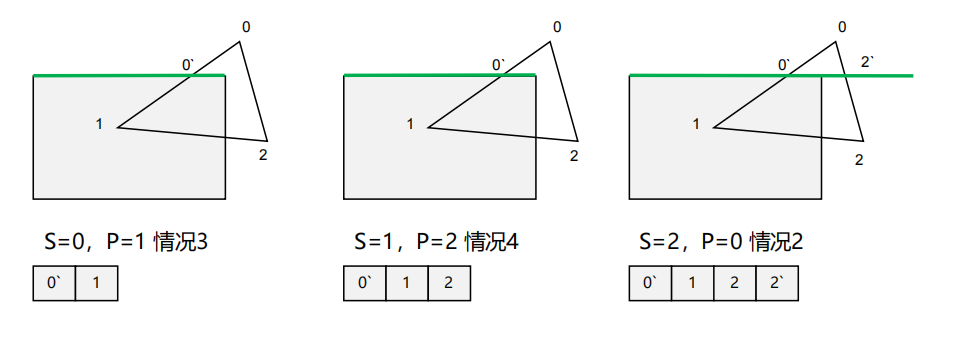
如法炮制考察剩余三边后，输出0`-1-2-2`

输入0`-1-2-2`考察右侧边

图-5

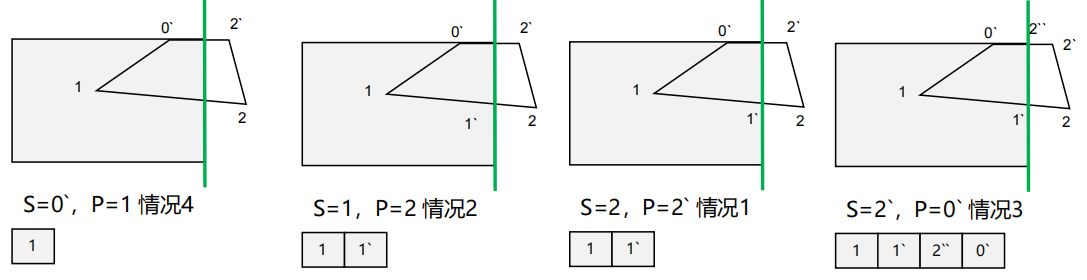
如法炮制考察剩余三边后，输出1-1`-2``-0`

对其他两条边如法炮制，最终可以获得下方所示数组：

图-6

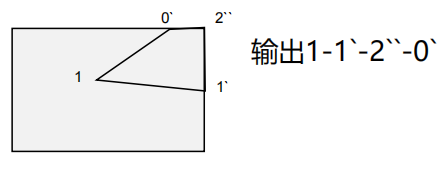
接下来进行三角形重建：永远以数组第一个顶点为起始点，递进构建三角形： 1-1`-2` 1-2``-0`

图-7

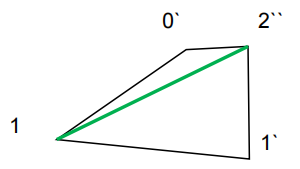
算法总结图解

图-8

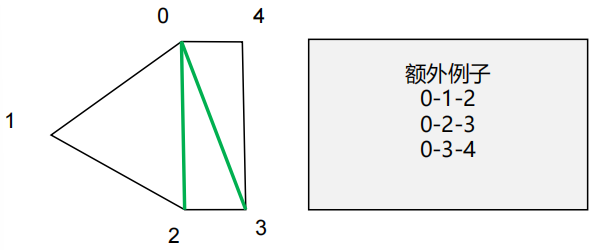
剪裁产生新点属性插值

当两个点位于平面内外两侧，我们需要对其进行插值，从而得到相交点的位置/颜色/uv等属性

图-9

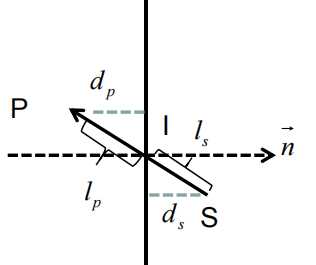
插值计算流程：
1.得到边界线的方程表达式
2.将p/s点代入求出边界距离
3.选择任何一条距离作为系数，执行线性插值

图-10

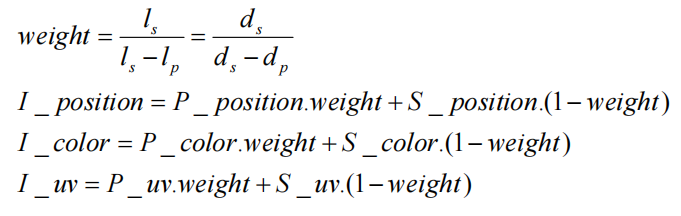
注意：L和d都是有方向的，Ls是正数，比上Ls-Lp,这个的Lp是负数，减去就相当于相加，所以就是和直线插值算法是一样的，改成投影方便计算

Sutherland-Hodgman算法（三维）

三维情况下，剪裁边变成了剪裁平面；我们选择在NDC构成的-1到1盒体内进行剪裁，但必须保证顶点在摄像机前方，顶点z值不为0（即不与摄像机重合）

图-11

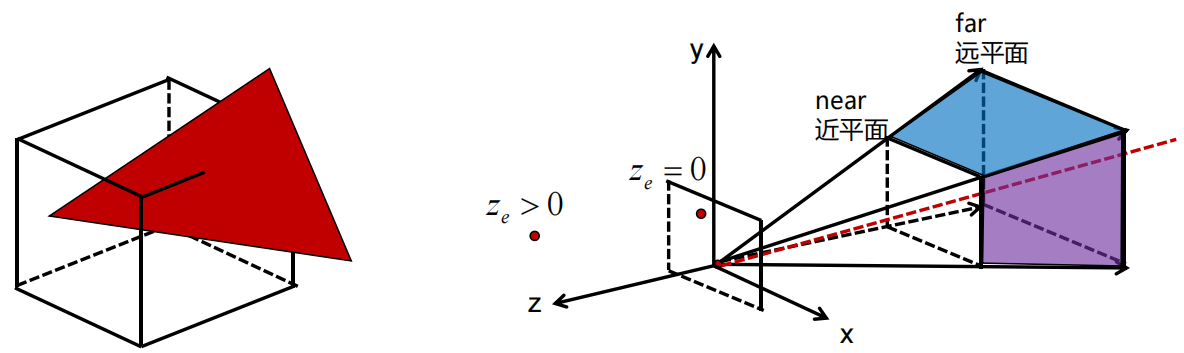
判定条件

根据上述条件以及NDC下坐标必须为-1到1内，可使用剪裁空间坐标对内外进行判定：

图-12

再将上面的判断条件展开，得到：

图-13

任意点代入方程后，得到的结果，都是距离判定平面的“有向距离”
插值交叉点的方法，也可采用前述的距离插值方法

Author: LYJ

Link: http://lyjseagull.github.io/graphics-opengl-44-windows/

高级渲染管线功能

2025-09-20

43-剪裁算法—前置几何知识

直线方程理解一般直线方程写作: 由此也存在直线方程写作: 上式可分解为向量点乘，向量(a,b)必须为归一化后的向量当向量n为单位向量，n向量乘以p向量得到的p向量是n向量方向的投影长度该表达式可理解为，p点是所有满足向量n投影长度为d的点集合直线方程距离理解直线表达式中的d发生变化的时候，意味着直线沿着法线n滑动点与直线的距离关系空间中任一点q，带入到直线方程，得到的结果都是q在n上的投影表示q在直线法线的一侧，即正面表示q在直线法线对侧，即背面平面方程空间中一平面，使用法线方式进行表示如下: 平面方程理解平面方程的d发生变化时，意味着平面沿着法线n方向滑动点与平面的距离关系表示q在平面法线的一侧，即正面表示q在平面法线的对侧，即背面

2025-09-22

45-剪裁算法代码实现

内容1.Clipper类以及sutherlandHodgman算法2.GPU绘制流程加入剪裁3.绘制示例 dataStructures.h#pragma once#include "../global/base.h"#include "../math/math.h"//VAO之中，用于描述属性读取方式的Descriptionstruct BindingDescription { uint32_t mVboId{ 0 }; size_t mItemSize{ 0 }; size_t mStride{ 0 }; size_t mOffset{ 0 };};struct VsOutput { math::vec4f mPosition{ 0.0f, 0.0f, 0.0f, 1.0f }; math::vec4f mColor;//此处颜色改为0.0...

2025-09-23

46-透视修正算法

插值算法回顾透视投影下，目前代码中，都是变化到屏幕空间坐标系后，按照屏幕空间形成的三角形对某点进行重心坐标插值：但是在三维空间中，三角形是立体有深度(前后)的图形，需要使用空间中的三角形重心坐标，使用屏幕上二维的重心坐标是不准确的问题分析（1）逆着y轴看下去，可以得到如下平面视图：由上图可知，在屏幕空间中，A`O`:B`O`=7:3在三维空间中，AO:BO=5:5可见两者的重心坐标并不相等，因此需要透视修正：为了能方便计算屏幕空间三角形像素的重心坐标，需要找到一种方法计算三维空间对应点的重心坐标问题分析（2）顶点到屏幕，会经历如下空间变换：我们已经知道三维空间投影到二维重心坐标会变换，那么N空间到S空间，对应点的重心坐标会发生变换吗？如上图分析，N空间到S空间，会发生两个变换：（1）顶点坐标从-1到1，变换为0-1，这个过程NDC内对应顶点重心坐标不会发生改变（2）顶点坐标从为0-1变化为屏幕上具体的像素点，并且由于width与height不同，产生了横向与纵向的拉伸，可以理解为，先投影到1*1的幕布上，然后横向统一缩放width倍...

2025-09-24

47-透视修正代码实现

内容1、修改了GPU中的透视除法函数2、加入剪裁函数trim3、加入透视恢复函数4、Raster插值，加入1/w以及depth5、主流程更改6、示例修改GPU中的透视除法函数dataStructures.h修改了GPU中的透视除法函数，添加了mOneOverW代表当前点的1/w #pragma once#include "../global/base.h"#include "../math/math.h"//VAO之中，用于描述属性读取方式的Descriptionstruct BindingDescription { uint32_t mVboId{ 0 }; size_t mItemSize{ 0 }; size_t mStride{ 0 }; size_t mOffset{ 0 };};struct VsOutput { float mOneOverW{ 0.0f }; math:...

2025-09-26

49-深度测试算法与代码实现

问题分析：在绘制两个三角形的过程中，系统如何决定谁遮挡谁？之前我们的设计是画家算法，即最早渲染的被最新渲染的遮挡，但不按照由远到近的顺序绘制时，就得不到我们像要的效果，如何直接根据图形的远近设置他们是否被遮挡，我们需要深度测试算法深度在屏幕空间变换后，我们得到的每个顶点的z坐标即顶点深度；在经过光栅化后得到的每个像素中都记录则经过插值的搭配的z值，即像素的深度值，用于描述当前像素距观察点有多远深度取值范围是0-1 深度检测：对于当前像素，都需要跟画布已有的像素深度值进行对比，如果被挡住则丢弃；如果靠前则保留深度缓存：跟画布一样分辨率大小的内存空间，用于记录画布上已经绘制的每个像素的深度值深度测试算法解析深度缓存与颜色缓存分辨率一致，初始化为1.0f 三角形每个像素深度值与深度缓存中对应深度值对比；如果三角形像素深度值较小（接近观测点）则通过测试；通过测试的像素，使用新的像素深度值覆盖对应的深度值；通过测试的像素，可以绘制到颜色缓存 API设计深度检测可配置参数较多，我们只选取深度对比函数进行编写：DEPTH_LESS: 代表比现存深度小才能通过检测DEPTH_GR...

2025-09-25

48-背面剔除算法与代码实现

剔除算法目的：提前丢弃对最终画面无贡献的三角形，减少不必要的渲染计算 OpenGL中，系统API允许设置三角形剔除：1、设置“正面”三角形的顶点连接方式（顺时针/逆时针）2、设置剔除“正面”还是剔除“背面” 举例：顶点逆时针连接维正面/剔除背面左手坐标系问题在NDC坐标中，已经变成了采用左手坐标系表示在左手坐标系中，向量叉乘必须采用左手来判定叉乘结果向量方向，例如：x与y叉乘，得到z 判定算法举例：逆时针为正面，剔除背面以0点为起点，与1点/2点构成两条边e1/e2求两向量叉乘，e1叉乘e2（左手坐标系）叉乘结果冲向屏幕内部，左手坐标系下，为z正方向，即z>0则使用z>0可判定该三角形可保留若如下图，顺时针排列顶点，e1与e2叉乘得到z<0，则可判定剔除该三角形总结以0点为起点，与1点/2点构成两条边e1/e2；计算e1与e2叉乘，得到其结果z值分条件判定：1、剪裁背面/逆时针为正面: z>0 保留2、剪裁正面/逆时针为正面: z<0 保留3、剪裁背面&#...