15-矩阵乘法行列视图
横看成岭侧成峰,矩阵和向量之间的权重配比关联?
【矩阵的列视图】
可将矩阵看成多个列向量排布构成:
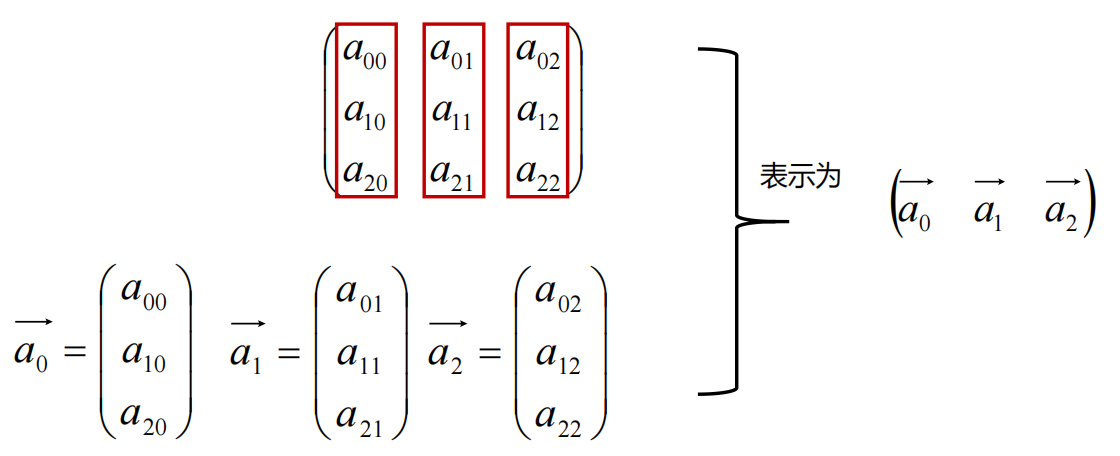
【矩阵的行视图】
也可将矩阵看成多个行向量排布构成:
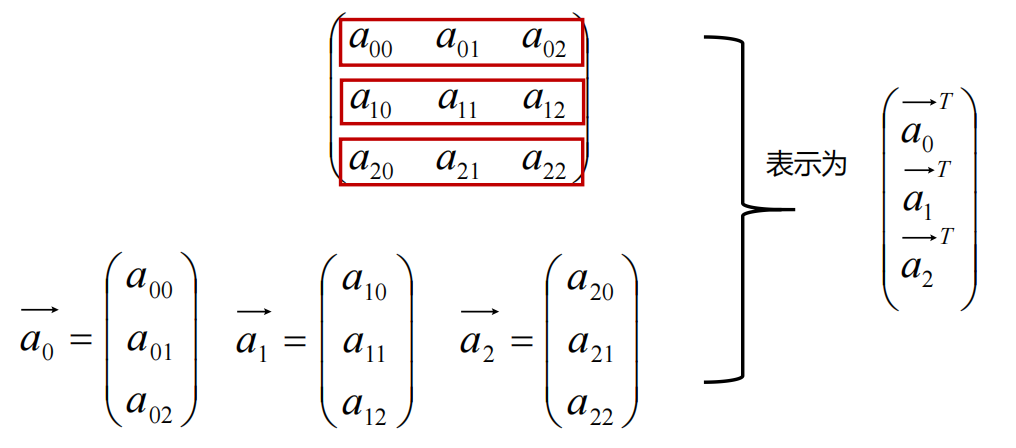
【矩阵乘法回顾,推演新的意义】
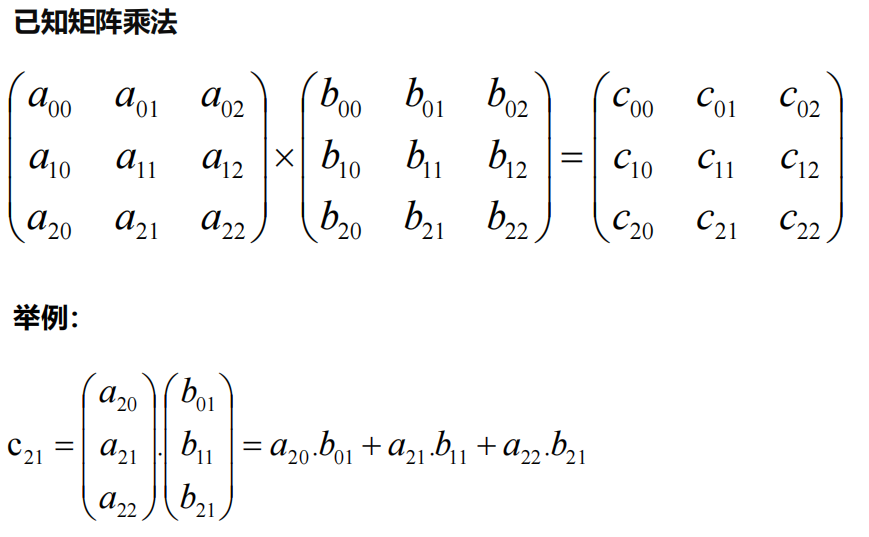
【用列视图看矩阵与向量相乘】
矩阵的每一列可理解为一个向量,乘法可看作三个向量的加权和
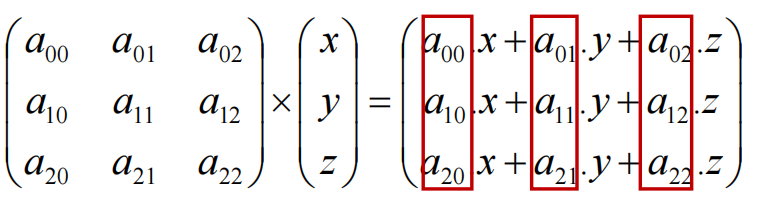
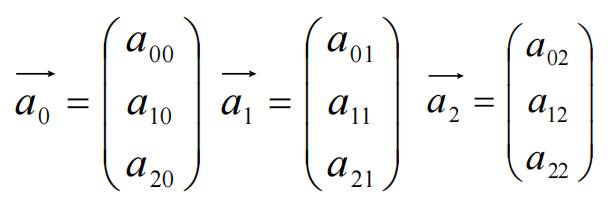
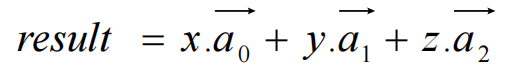
【用列视图理解矩阵乘法】
A矩阵看作列向量的组合,结果C矩阵也可看作列向量的组合
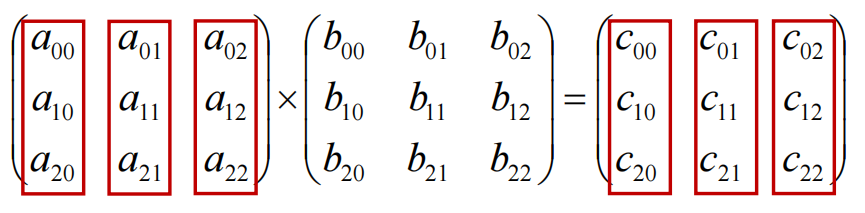
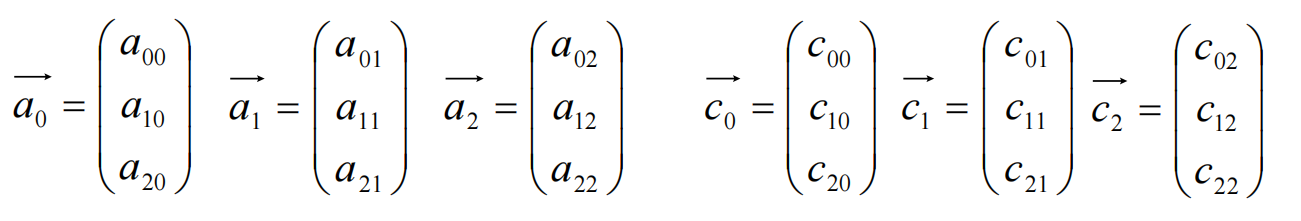
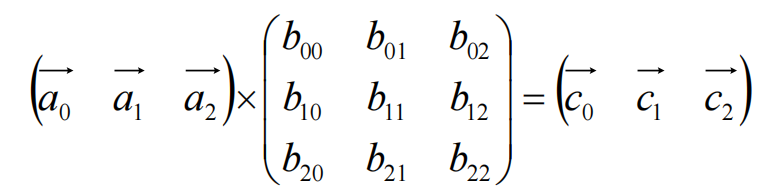
按照矩阵乘法就可以得到下面的等式,
这个可以看作: 矩阵B的每一列元素是矩阵A的列向量的调配比例(权重);
结果矩阵C的每一个列向量是通过矩阵A列向量权重加和得到的
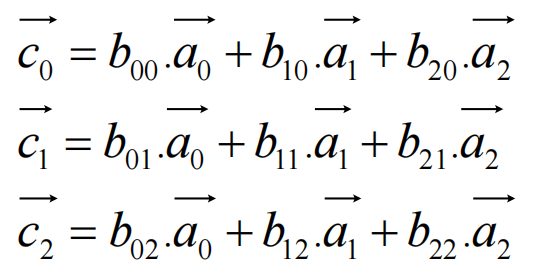
【用行视图看矩阵与向量相乘】
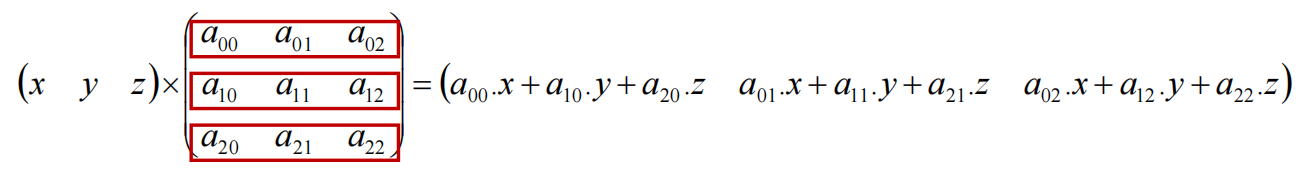
矩阵每一行可理解为一个向量,乘法可看作三个行向量的加权和
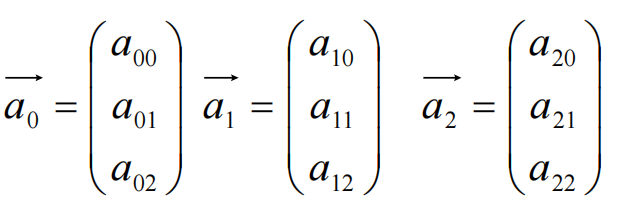
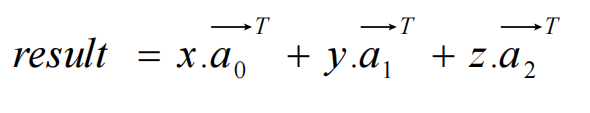
【用行视图理解矩阵乘法】

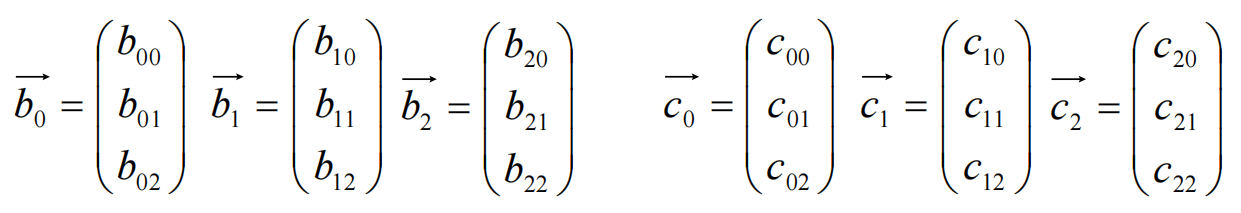
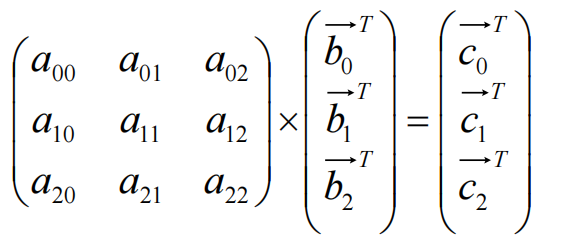
按照矩阵乘法,矩阵A的每一行都可理解为矩阵B的行向量的调配比例(权重);
结果矩阵C的每一个行向量都是矩阵B根据A提供的权重加权相加得到的
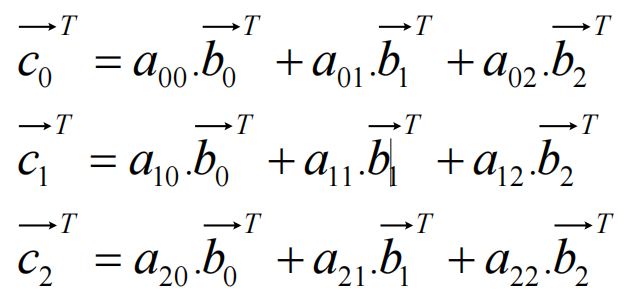
All articles on this blog are licensed under CC BY-NC-SA 4.0 unless otherwise stated.
