16-矩阵行列式计算
行列式
行列式有多种几何意义: 如,平行多面体的体积;方便得到矩阵的逆矩阵等。因此学习行列式大有用处。
行列式的定义
矩阵行列式被称为det,是基于矩阵所包含的行列数据计算得到的标量;本质上是一个数;只有方阵拥有行列式。


行列式的由来
历史上做行列式是为了求解方程组的解,使用克莱姆法则,先将方程组写为矩阵的形式:
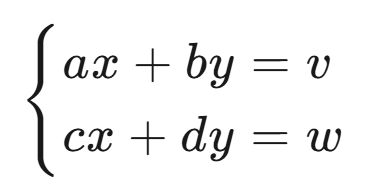
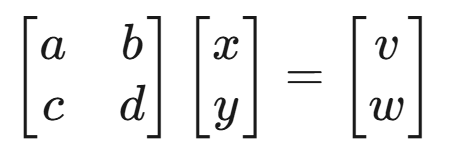
记系数矩阵为:
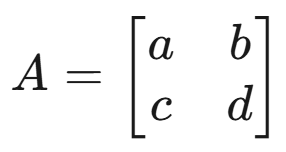
其行列式就是:
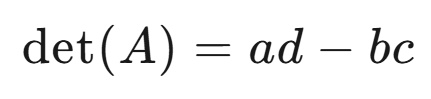
根据克莱姆法则有:
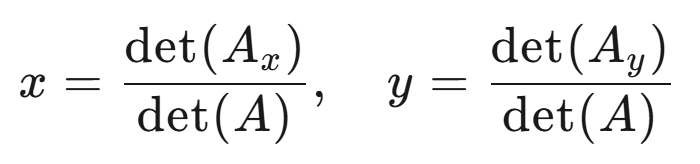
其中:
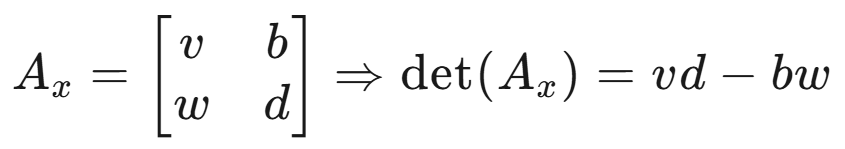
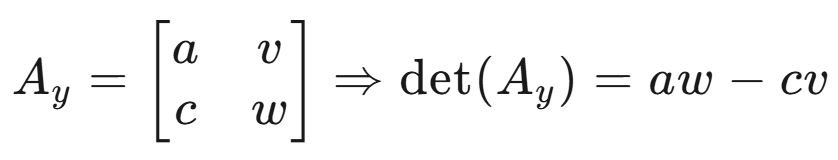
最终得到:
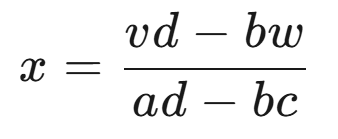
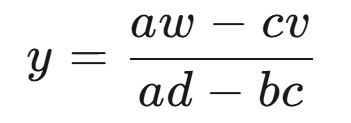
分母部分都是统一的;且形式上就是标准的二维行列式;同样的理解方式可以推广到三元一次方程组的解,三维矩阵的行列式即其解的分母。

根据克莱姆法则真是一个古老的算法,一个很直观的法则
怎么求行列式?
行列式求值工具————排列
(1)排列:由1,2,3,4…n组成的一个有序数组,称为n级排列(中间不能缺数)
(2)逆序:大数排在小数前面记为一次逆序
(3)逆序数:一个排列中,逆序的总数;用符号N表示
(4)举例:

行列式计算定义(按行展开)
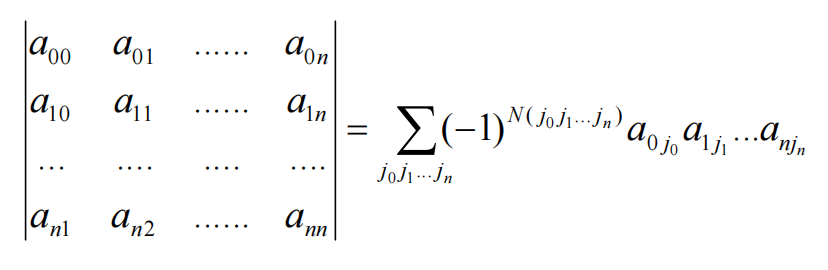

同样也可以按列展开:
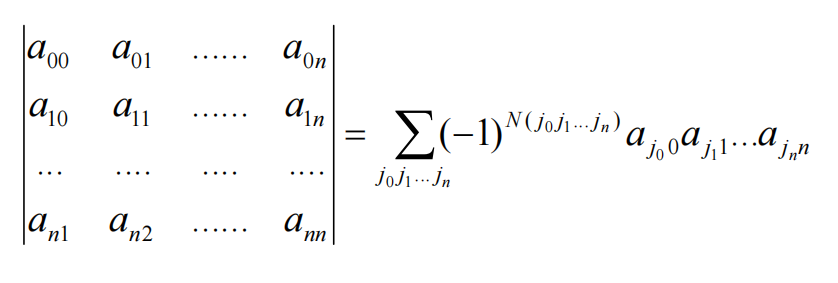
All articles on this blog are licensed under CC BY-NC-SA 4.0 unless otherwise stated.
