17-矩阵行列式的基本性质
行列式基本性质 (一)
对于矩阵A,其行列式满足: 矩阵转置后行列式不变
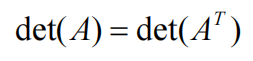
Think: 转置就是行变列,列变行;转置前按列展开求行列式,转置就变为按行展开行列式,依据“16-矩阵行列式计算”我们知道他们的行列式是一样的
行列式基本性质 (二)
对于矩阵A,其行列式满足:更换两行数据位置,行列式绝对值不变,符号变号;
理解: 对于排列S,更换排列中的两个数字,S的逆序数改变奇偶性

行列式基本性质 (三)
如果矩阵A(方阵)中有两行或两列数据相同,则det(A)=0
理解: 根据性质(二),更换矩阵A中的两行数据后得到A`,行列式绝对值不变,符号变号,于是det(A)=-det(A`);同时因为交换了两行相同的数据,所以矩阵A实际就是矩阵A`,两个行列式相等,det(A)=det(A`);所以det(A)=0
行列式基本性质 (四)
对于矩阵A,任一行数据共同乘以c,则行列式为det(A)*c
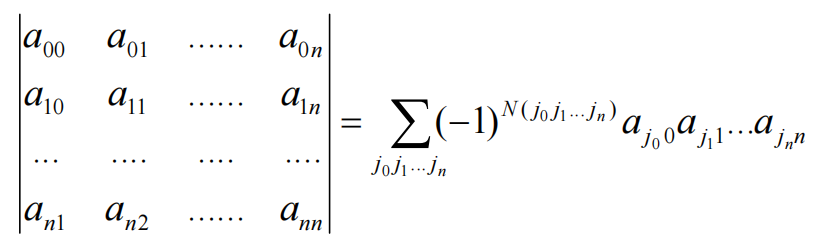
理解: 使用按列展开,某一行数据乘以c,则每个连乘项当中都会包含一个本行数据,则都会共同乘以c,可提到外部
行列式基本性质 (五)
对于矩阵A,某一行数据加在另一行数据上,得到A`,det(A)=det(A`)

理解: 按列展开,可观察到其中某一项(主对角线)为 1*1*(2+1) = 1*1*2 + 1*1*1,行列式可拆解为:
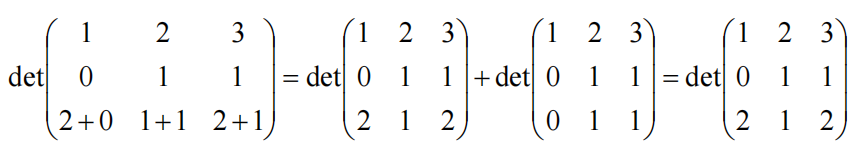
可以看到第二项有两行相同的数据,更具性质三,第二项行列式为0,最终得到的与原行列式相同
行列式基本性质 (六)
对于矩阵A,某一行数据乘以数字c,加到其他行上,得到A`,det(A)=det(A`)

理解: 按列展开,观察其中一项(主对角线): 1*1*(2+1*3) = 1*1*2 + 1*1*(1*3),行列式可拆解为:
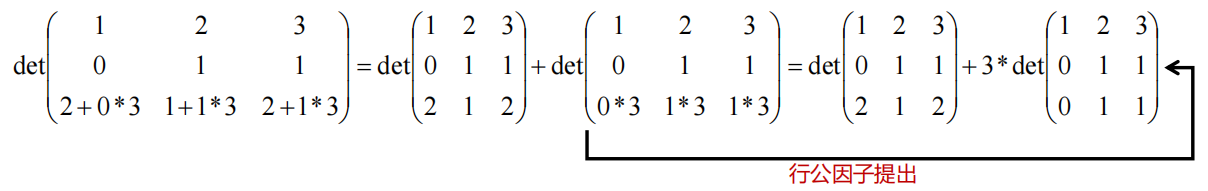
行列式————补充性质
对于同阶矩阵A、B,其行列式满足:
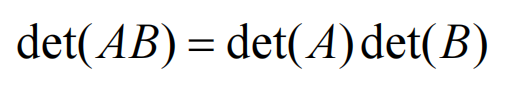
在后续学习矩阵的空间变换后可加深对这个性质的理解
行列式性质总结提炼
对于矩阵A,其行列式满足:
1、任何一行数据,共同乘以c,行列式为det(A)*c
2、更换两行数据位置,行列式绝对值不变,符号变号
3、单位矩阵的行列式为1
4、某一行数据乘以某一数字c,加到其他行上,行列式不变
行列式计算的另一种定义方式
对于矩阵A,定义一种运算F(A),满足:
1、任何一行数据,共同乘以c得到A`,则F(A`)=F(A)*c
2、更换两行数据位置得到A`,则F(A`)=-F(A)
3、如果A是单位矩阵,则F(A)=1
4、某一行数据乘以某一数字c,加到其他行上,得到A`,则F(A`)=F(A)
也就是说,如果存在一种运算F,满足行列式的这4个基本性质,那么F运算得到的结果即为矩阵A的行列式
