25-空间变换—任意轴旋转
回顾列视图矩阵
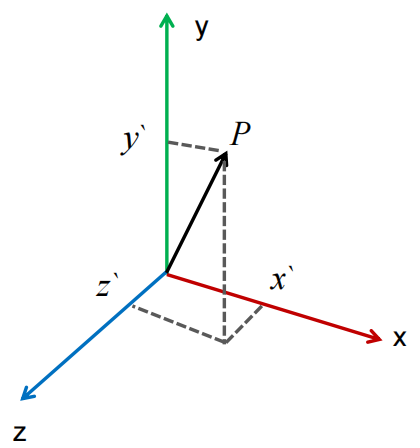
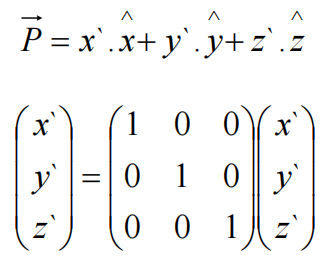
理解:向量P由矩阵的三个列向量分别乘以向量x/y/z 的分量后,再加和得到;列向量形成的矩阵可理解为x/y/z的权重因子,它影响着向量P的指向与长度。
旋转的几何理解
对于任意的旋转操作矩阵,假设存在以下计算:
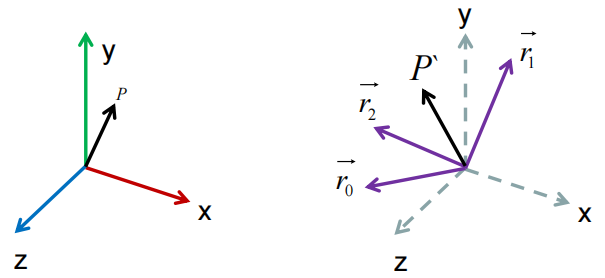
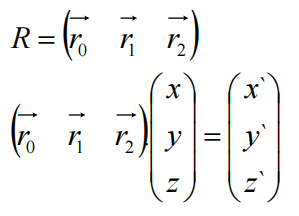
由矩阵列视图可看作:
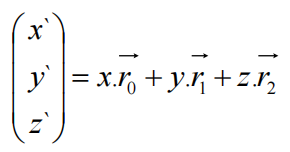
理解: 旋转变换矩阵,内部的三个列向量就是新坐标系R的三个基向量,按序对应与X/Y/Z轴;
P相对于新坐标系R的位置不变,通过对R的基向量进行加权加和,就可以计算变动后的P的原坐标系位置;
也可理解为把原来的坐标系进行旋转得到新的坐标系R,P跟着一起旋转,但是相对于R位置不变
旋转的几何理解——延申
如果已知一个旋转矩阵A,可以通过与基向量相乘,求出每一列
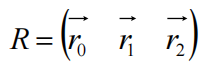
令其与x/y/z轴向量分别相乘,即可求出对应列
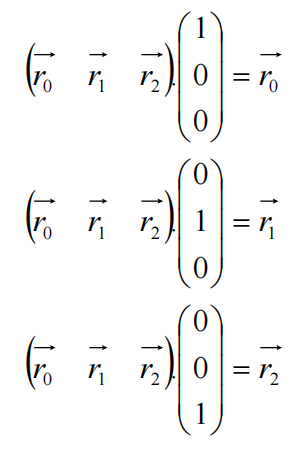
绕任意轴旋转推导
已知旋转轴为u,v围绕旋转角,得到v`,求v`的坐标表示
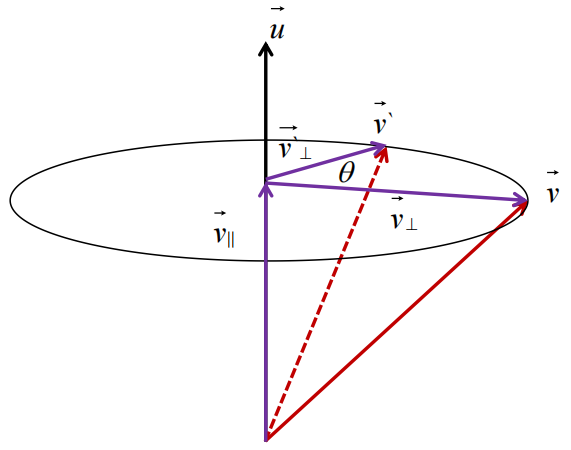
思路:(先保证向量u是归一化后的单位向量)

求向量v在向量u上的投影向量 v平行向量:
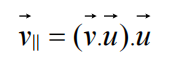
求垂直向量u的向量 v垂直向量:
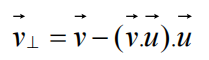
观察顶部截面,需要求v`垂直向量 还需要构造纵坐标向量w
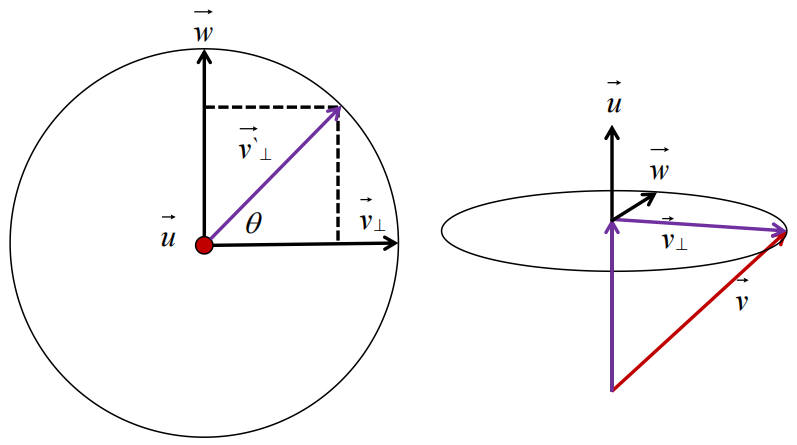
旋转是逆向旋转轴看,逆时针旋转;
看向旋转轴是,其余两轴向上/右延申为正;
依据上述右手坐标系规则,可以得到其计算方法:(向量w与向量 v垂直相同)
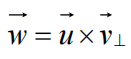
求向量v`垂直:
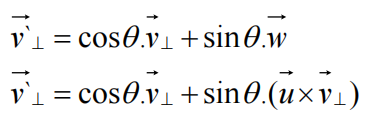
整理公式得:
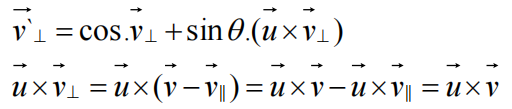
最终公式代入:
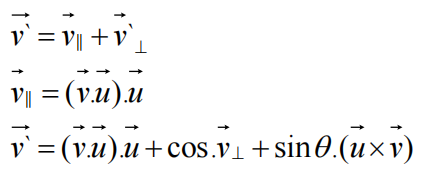
由于:
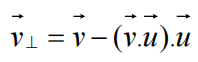
可知:
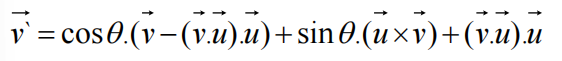
现在,回到“旋转几何理解——延申”,我们知道:
令v=(1,0,0) 可得到矩阵的第一列; 令v=(0,1,0)可得到矩阵的第二列; 令v=(0,0,1)可得到矩阵的第三列举例:
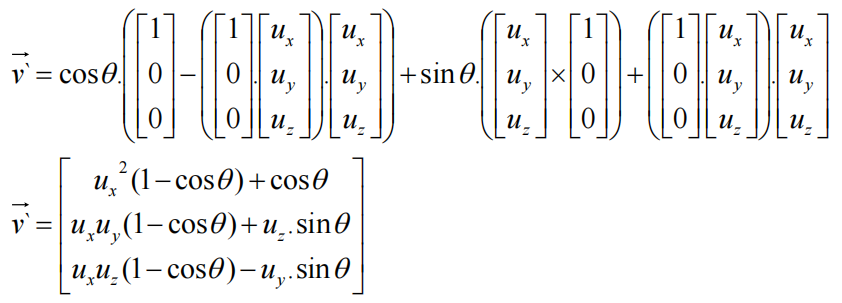
旋转矩阵的最终面貌
已知旋转矩轴为u, v围绕其旋转θ角,其旋转矩阵如下:
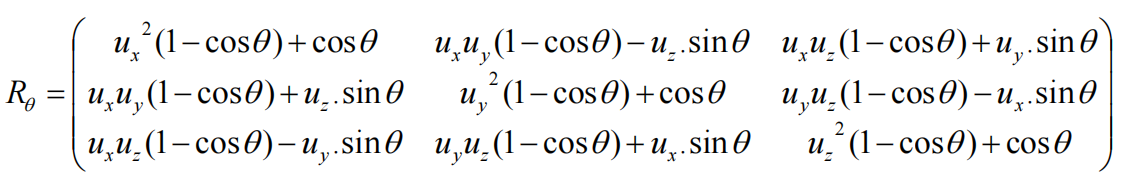
All articles on this blog are licensed under CC BY-NC-SA 4.0 unless otherwise stated.
