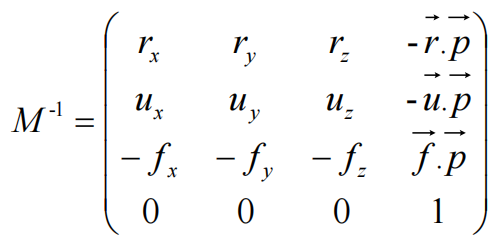26-空间变换—视图变换
摄像机定义
在渲染技术中,如果坐标系确定以及物体都已经摆放完毕的情况下,需要确定一台摄像机,描述观察者的参数
摄像机相关参数:
1、摄像机位置
2、摄像机看向的方向
3、摄像机穹顶方向
4、摄像机视张角: 模拟人的眼睛张开的角度,在屏幕上显示的效果就是显示图像局部或整体的样子
摄像机初始状态
我们的目标是确定摄像机当前看到的场景,即观察者在摄像机的位置,看向的方向
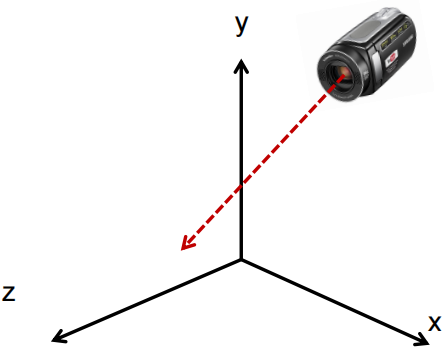
最简单的情况如下,摄像机就在坐标原点
摄像机相关参数:
1、摄像机位置摆放在坐标系原点
2、摄像机看向的方向是负Z轴方向
此时可以直接进行投影计算操作,所有舞台沿Z轴投影到摄像机的幕布上,相对简单
摄像机变化状态
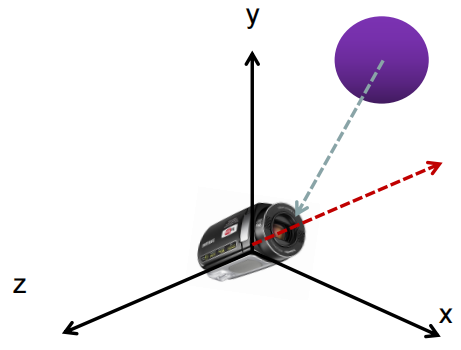
如果摄像机经过旋转平移等操作,变成如下形态:
如下图,可通过施加旋转变换矩阵和平移变换矩阵恢复到原点
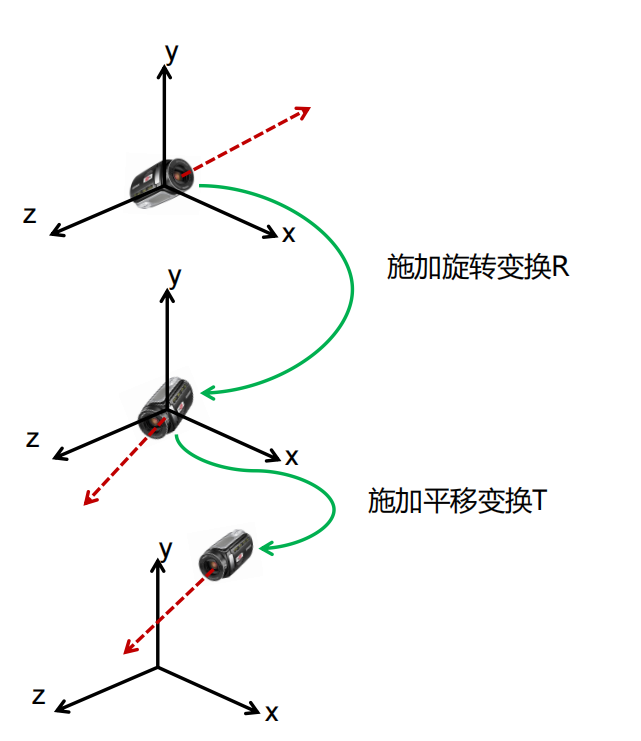
摄像机变换——逆变换
已知摄像机是由R与T结合的,所以最终变换矩阵为M=T*R(注意变换顺序)
逆变换: M矩阵的逆矩阵可以把摄像机从变换后的状态“恢复”到初始化的状态
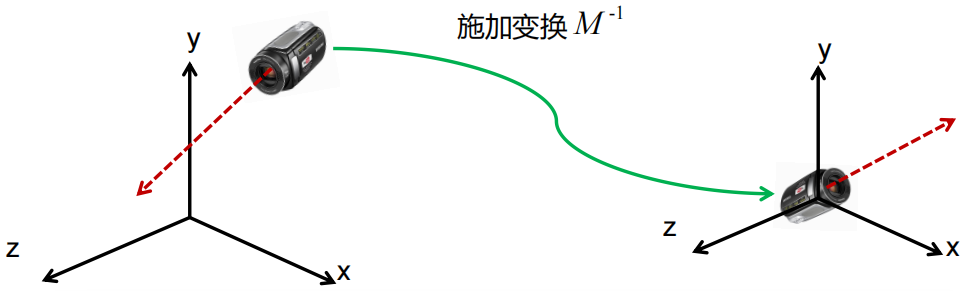
相对不变准则
思路: 最终目的是将图像投影到摄像机,所以把摄像机跟场景物体做同样的矩阵变换,则显示关系不变
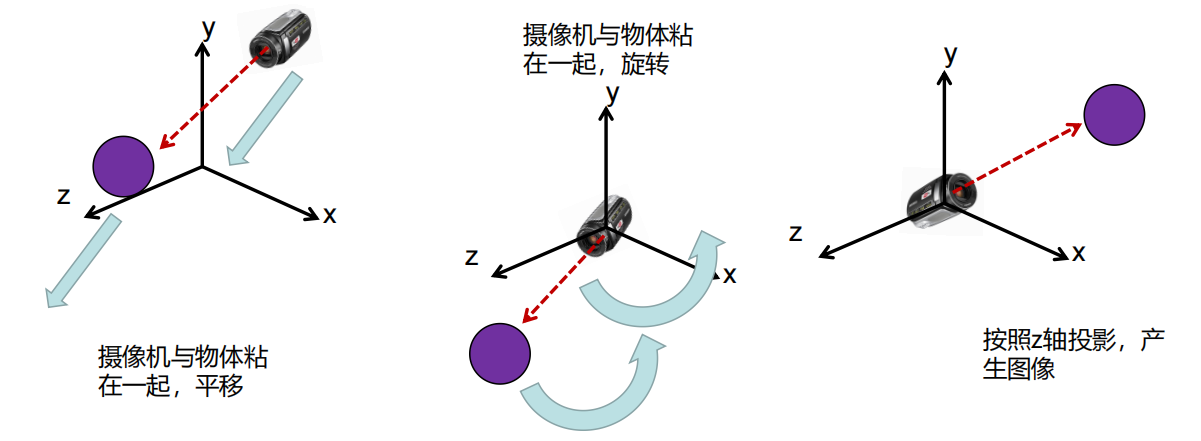
对摄像机使用M逆矩阵后,摄像机就处于原点,看向-Z方向;
与此同时,对场景中所有物体都使用M矩阵进行变换,则所有物体与摄像机相对位置就不会发生变化
构建摄像机矩阵
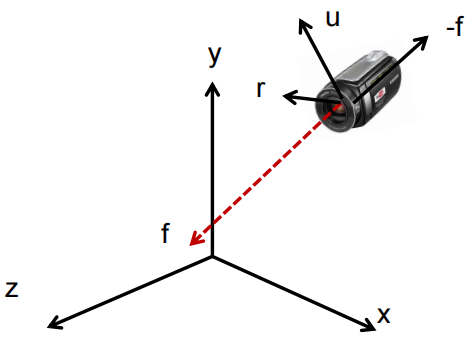
目标: 根据已知条件求M矩阵,把摄像机变换到当前状态
条件:已知当前摄像机看向的方向,称作front向量(front必须归一化),以及摄像机位置P
原理回顾:旋转变换矩阵的三列向量,其实是新坐标系基向量的三个轴,分别对应原来的X/Y/Z
摄像机坐标系的-z即f向量已知,顶部u向以及右边r向量均未知
规定顶部向量
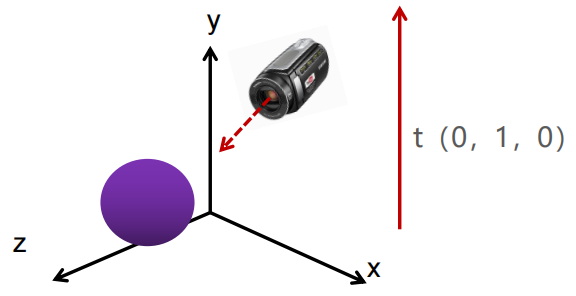
对于一台摄像机,在固定好位置与方向之后,会产生两种情况,如下图:
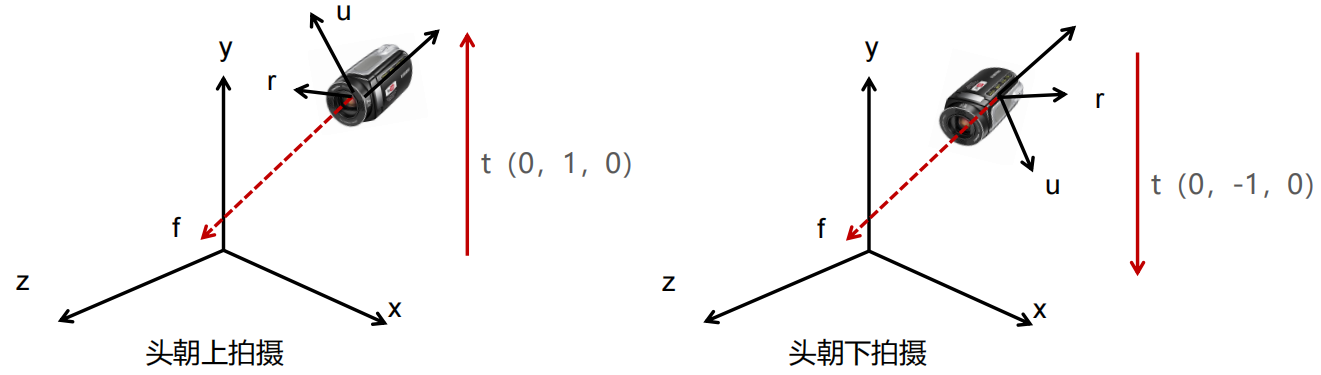
所以需要提前规定顶部向量,左图是(0,1,0).右图是(0,-1,0)
构建右侧向量r与头顶向量u
已知方向向量f以及顶向量t,可知:
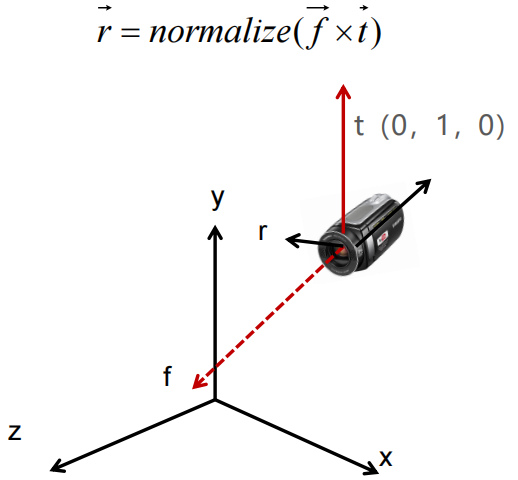
已知方向向量f以及右部向量r,可知:
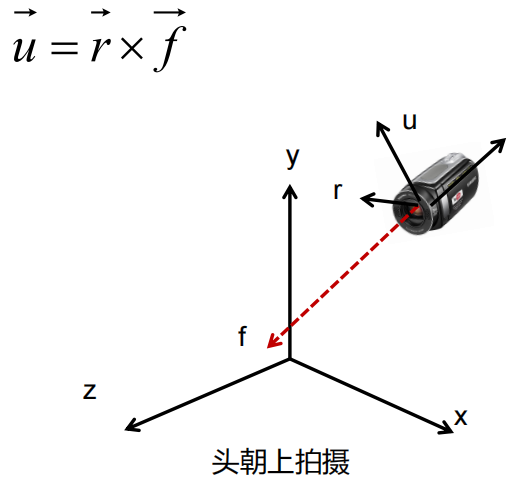
构建旋转矩阵
目前已知摄像机坐标系下的X/Y/Z轴分别为: r u -f
可以构建如下旋转矩阵以及其逆矩阵(旋转矩阵都是正交阵)
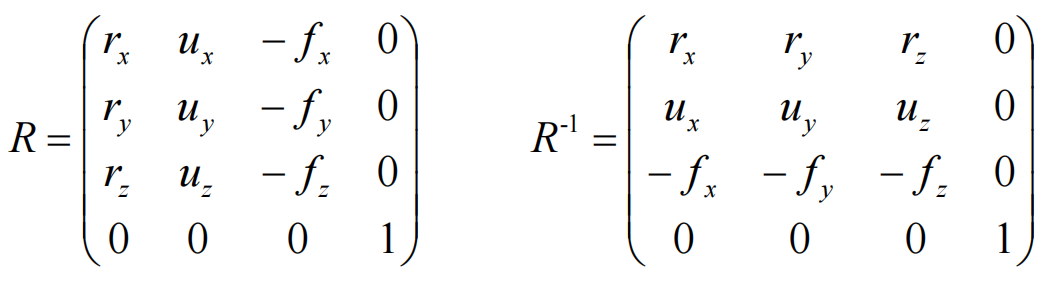
构建平移矩阵
目前已知摄像机位于点P位置
可以构建如下平移矩阵以及其逆矩阵
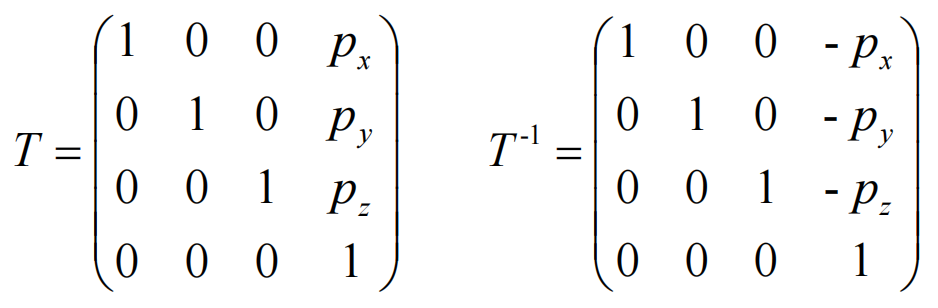
构建视图变换矩阵(View Matrix)
View Matrix即摄像机变换到目标状态的逆矩阵,作用是将摄像机变换回初始状态
摄像机变换到目标状态的矩阵为:
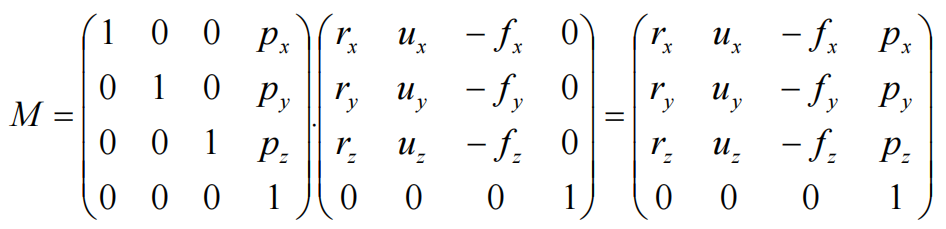
摄像机回归到初始状态的矩阵为:
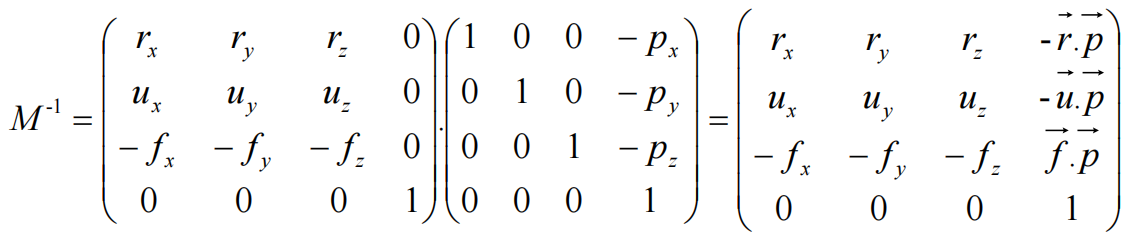
结论
摄像机拥有自己的变换矩阵M,将其变换到目标位置以及旋转状态
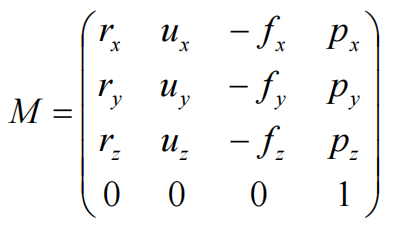
视图矩阵为M的逆矩阵,施加在所有物体上,将他们变换到摄影机坐标系,从而可达到Z轴投影的目的